Question

When you answered the question can you please put it the inter- where it belongs for example tell me where is the Y intercept answer and what is the X intercept answer

Answer 1

Given:

`4x-3y=12`

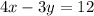
The y-intercept is the point where the line crosses the y-axis, at this point the x-coordinate is equal to zero. To find the corresponding y-coordinate, you have to replace the equation by x=0 and solve for y:

`\begin{gathered} 4x-3y=12 \\ 4\cdot0-3y=12 \\ 0-3y=12 \\ -3y=12 \end{gathered}`

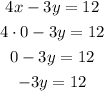
Divide both sides by -3

`\begin{gathered} (-3y)/(-3)=(12)/(-3) \\ y=-4 \end{gathered}`

The y-intercept is (0,-4)

The x-intercept is the point where the line crosses the x-axis, at this point, the y-coordinate is zero. To find the x-coordinate of the x-intercept you have to replace the equation with y=0 and solve for x:

`\begin{gathered} 4x-3y=12 \\ 4x-3\cdot0=12 \\ 4x=12 \end{gathered}`

Divide both sides by 4

`\begin{gathered} (4x)/(4)=(12)/(4) \\ x=3 \end{gathered}`

The x-intercept is (3,0)