N 8
we have the function
![g(x)=\frac{1}{\sqrt[]{16-x^2}}](https://img.qammunity.org/2023/formulas/mathematics/college/m0j9dgruz9imgtk7ygio83yufq7fevczu0.png)
Remember that
the denominator cannot be equal to zero and the discriminant must be greater than or equal to zero
that means
16-x^2 > 0
solve for x
-x^2 > -16
multiply by -1 both sides
x^2 < 16
the solution is the interval (-4,4)
therefore
In this problem
the domain is the interval (-4,4)
Step-by-step explanation
the domain is (-4,4)
If you put in the given function x=4
![g(x)=\frac{1}{\sqrt[]{16-4^2}}=(1)/(0)](https://img.qammunity.org/2023/formulas/mathematics/college/e5iu2jdhoy3pd7q9oyywf6i7k0pfhy6mxf.png)
undefined
If you put x=5
![g(x)=\frac{1}{\sqrt[]{16-5^2}}=\frac{1}{\sqrt[]{-9}}](https://img.qammunity.org/2023/formulas/mathematics/college/y3tr9i5n5q8mpzckniuldv32wh2m3v7npg.png)
is not a real number
For that reason, the domain is the interval (-4,4)
x^2 < 16
square root both sides
we have
(+/-)x < 4 -----> two inequalities
First
+x <4
second
-x <4 -----> x >-4
the solution is the compound inequality
x <4 and x> -4
we have the problem
![f(x)=\sqrt[]{16-x^2}](https://img.qammunity.org/2023/formulas/mathematics/college/97awr35gytpk59cwogqcs9fyxl5oqab8o6.png)
In this case
the radicand must be greater than or equal to zero
so
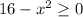
in this case
the domain is the interval [-4,4]
the value of x=-4 and x=4 are included in the domain because the function can be equal to zero
In the previous problem, the values of x=-4 and x=4 are not included, because the function cannot be equal to zero