Step-by-step explanation
We need to find the factored form of the polynomial:
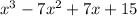
It's factored form should look like this:
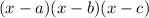
Where a, b and c are the zeros of the polynomial i.e. the x-values for which the polynomial is 0. When we have to find the zeros of a 3rd degree polynomial (i.e. a polynomial where the greatest power of x is x³) we can use Ruffini's Rule. The first step of this rule is to identify a zero of the polynomial from all the possible combinations given by dividing the dividers of the independent term by the dividers of the leading coefficient. The leading coefficient is the number multiplying x³ and the independent term is the number that is not multiplied by any power of x. These two numbers are 1 and 15 so we must find all the numbers formed by dividing the dividers of 15 and those of 1. First we list the dividers:
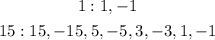
So we list all the quotients between the numbers in the second row and those in the first row:
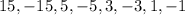
So one of these is a zero of the polynomial, let's test each of them:

So -1 is a zero. Now that we found one of its zeros the next step of Ruffini's Rule implies performing a long division between our polynomial and x-(-1). Rememeber that for a long division we must draw two parallel lines. The zero x=-1 must be written at the left of the vertical line and above the horizontal line. At the right of the vertical line we write the coefficients of our polynomial which are 1, -7, 7 and 15:
The first coefficient is also written below the horizontal line. Now we take that coefficient, we multiply it by the zero of the polynomial in the left side of the vertical line and we write the result below the second coefficient. Then we add the second coefficient and the result of the product and we write the new result below the horizontal line. So basically we calculate 1*(-1)=-1 and the resulting -1 is written below the -7. Then we add them: -7-1=-8. This result goes below the horizontal line:
Now we do the same procedure but with -8. We first multiply it by 1: -8*(-1)=8. We write this result below the third coefficient 7 and we add them: 7+8=15. And we write that 15 below the horizontal line:
And we repeat the process for the last time:
The three non-zero numbers below the horizontal line are the coefficients of a 2nd degree polynomial that multiplied by (x-(-1))=(x+1) are equal to the original polynomial. Then we get:
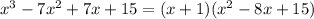
So the other two zeros of the polynomial are those of the 2nd degree polynomial in the right side. Remember that for a 2nd degree polynomial ax²+bx+c its zeros are given by:

In this case a=1, b=-8 and c=15 so we get:
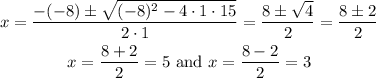
So the zeros of this expression are x=3 and x=5. Then we have the three zeros of the original polynomial x=-1, x=3 and x=5. So the factored form is:

Answer
Then the answer is option C.