We have got the function:
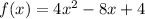
If we want to calculate:
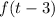
We can simply substitute every "x" in the function with "t-3". We need to use parenthesis when we do that:
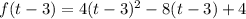
To get an answer that corresponds to one of the alternatives, we will need to simplify. First, let's solve the square and the parenthesis:
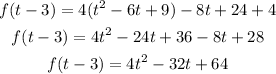
This corresponds to alternative 1.