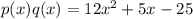Question

Let p(x) = 3x + 5 and g(x) = 4x 5. Finda. p(x) - q(x) =b. p(x) + g(x) =c. p(x)q(x) =

Answer 1

Step-by-step explanation:

Given that

`p(x)=3x+5,q(x)=4x-5`

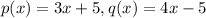
Part A:

Find

`p(x)-q(x)`

By substituting the values, we will have

`\begin{gathered} p(x)-q(x)=3x+5-(4x-5) \\ p(x)-q(x)=3x+5-4x+5 \\ p(x)-q(x)=3x-4x+5+5 \\ p(x)-q(x)=-x+10 \\ p(x)-q(x)=10-x \end{gathered}`

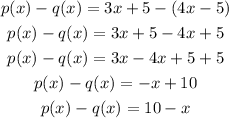
Hence,

The final answer is

`p(x)-q(x)=10-x`

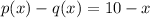
Part B:

Find,

`p(x)+q(x)`

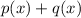
By substituting the values, we will have

`\begin{gathered} p(x)+q(x) \\ p(x)+q(x)=3x+5+4x-5 \\ p(x)+q(x)=3x+4x+5-5 \\ p(x)+q(x)=7x \end{gathered}`

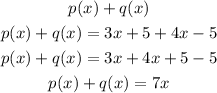
Hence,

The final answer is

`p(x)+q(x)=7x`

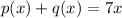
Part C:

Find,

`p(x)q(x)`

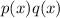
By substituting the values, we will have

`\begin{gathered} p(x)q(x)=(3x+5)(4x-5) \\ p(x)q(x)=3x(4x-5)+5(4x-5) \\ p(x)q(x)=12x^2-15x+20x-25 \\ p(x)q(x)=12x^2+5x-25 \end{gathered}`

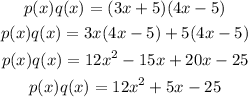
Hence,

The final answer is

`p(x)q(x)=12x^(2)+5x-25`