Since the angle at point P is a right angle, the triangle is a right triangle.
And since this is a right triangle, we can use the Pythagorean theorem:
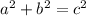
Where a, and b are the legs of the triangle, and c is the hypotenuse of the triangle.
In this case, the legs of the triangle are PR and PQ, and the hypotenuse is RQ, so the Pythagorean theorem for this triangle is as follows:
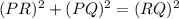
We know from the image that:
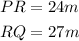
So we substitute this in the Pythagorean theorem:
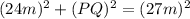
squaring the quantities we get:
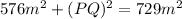
The width of the pond is PQ, so we need to solve for PQ in the equation.
To solve for PQ we subtract 576 to both sides:
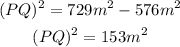
Finally, to find PQ, take the square root of both sides of the equation:
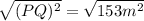
On the left side, we just get PQ and on the right side we get the square root of 153 which is 12.369:
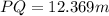
Answer:
The width of the pond is:
![\sqrt[]{153}m=12.369m](https://img.qammunity.org/2023/formulas/mathematics/college/v8vjp71g5ph5x087q4q5z1309es2sl0kkw.png)