Question

A hot bowl of soup cools according to Newton’s law of cooling. Its temperature (in degrees Fahrenheit) at time t is given by T(t) = 66 + 144e-0.04t, where t is given in minutes.How long will it take for the soup to cool to a temperature of 120°F? Round your answer to the nearest tenth of a minute

Answer 1

Given:

The temperature (in degrees Fahrenheit) at time t is given by

`T(t)=66+144e^(-0.04t)`

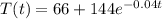
Required:

We need to find the time when the soup to cool to a temperature of 120°F.

Step-by-step explanation:

Substitue T(t)=120 in the equation to find the value of t.

`120=66+144e^(-0.04t)`

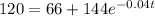
Subtract 66 from both sides of the equation.

`120-66=66+144e^(-0.04t)-66`

`54=144e^(-0.04t)`

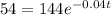
Divide both sides by 144.

`(54)/(144)=(144e^(-0.04t))/(144)`
`0.375=e^(-0.04t)`

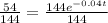
Take natural log on both sides of the equation,

`In(0.375)=-0.04t`

`-0.9809=-0.04t`

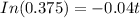
Divide both sides by (-0.04).

`(-0.9809)/(-0.04)=(-0.04t)/(-0.04)`

`24.5225=t`

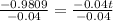
Round of the nearest tenth of a minute.

`24.5=t`

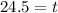
We get t =24.5 minutes.

Final answer:

It takes 24.5 minutes for the soup to cool to a temperature of 120°F.