We have a graph that relates the number of games with the total yearly cost.
The graph only shows results for up to 6 games, so we have to find the equation of the line to extrapolate it to 10 games.
We can find the equation of the line in slope-intercept form:

where y is the yearly total cost and x is the number of games.
The y-intercept b is the value of y when x=0. We can see it in the graph: when x=0 (no games), the yearly cost is $90.
So b=y(0)=90.
We can find the slope in many ways now, but we will find it by replacing x and y with known values of a point of the graph, like (x,y)=(1,120), that is the point that indicates that 1 game (x=1) costs a total $120 (y=120).

The slope has a value of m=30.
Then, we have the equation as:
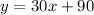
We can find the cost of joining and playing 10 games by replacing x with 10 and calculating for y:

Answer: $390