Question

The table below shows the relationship between x and y

Answer 1

Given the table showing the relationship between x and y, below:

We can represent the relationship between x and y using the equation of a line expressed as

`\begin{gathered} y=mx+c\text{ ----- equation 1} \\ where \\ m\Rightarrow slope\text{ of the line} \\ c\Rightarrow y-intercept\text{ of the line} \end{gathered}`

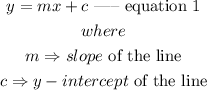
step 1: Evaluate the slope m of the line.

The slope m of the line is expressed as

`m=(rise)/(run)=(y_2-y_1)/(x_2-x_1)\text{ ----- equation 2}`

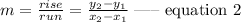
To find the equation of the line, we select two points (x, y) from the table of values.

Thus, selecting the points (-1,-1) and (0,1), this implies that

`\begin{gathered} x_1=-1 \\ y_1=-1 \\ x_2=0 \\ y_2=1 \end{gathered}`

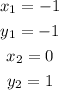
Substituting these values into equation 2, we have

`\begin{gathered} m=(1-(-1))/(0-(-1)) \\ =(1+1)/(0+1) \\ =(2)/(1) \\ \Rightarrow m=2 \end{gathered}`

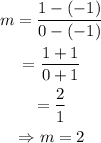
step 2: Evaluate the y-intercept of the line.

The y-intercept of the line is the value of y when the line cuts the y-axis. In other words, it's the value of y when the value of x equals zero.

In the table of values, when the value of x equals zero, the value of y is 1.

Thus, the y-intercept of the line is

`c=1`

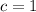
step 3: Substitute the values of m and c into equation 1.

From equation 1,

`\begin{gathered} y=mx+c \\ where \\ m=2,\text{ c=1} \end{gathered}`

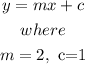
Thus, the function that represents the relationship between the quantities in the table is

`y=2x+1`

The correct option is F.