To find the number of molecules, we first need to find the number of moles.
To do that, we need the molar mass of N₂O, which we can calculate using the molas masses of the elements in it:
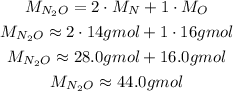
To convert from mass, m, to number of moles, n, we will use the following:
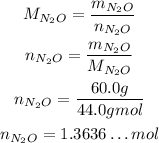
And to convert from number of moles to number of molecules, we use the Avogadro's number:
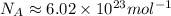
So:
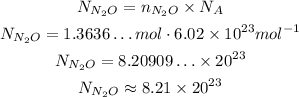
So, the number of molecules in 60.0 g of N₂O is approximately 8.21 x 10²³.