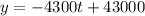Since two points define a line, we can take two points through which the line passes and find its equation.
From the word problem, we know that when t = 0, the original value is equal to $43,000. Then, we have a first ordered pair.
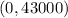
Since the value is reduced by $4300 each year, we have a second ordered pair.
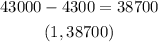
Now, we find the slope of the line using the following formula.
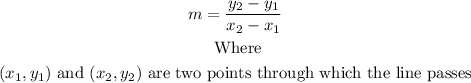
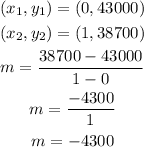
Finally, we can use and solve for y the point-slope formula.
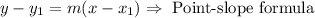
Since the situation described depends on the time t, we replace x with t in the formula.
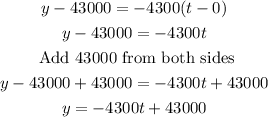
Therefore, the linear equation that models the value y of the machinery at the end of year t is: