Question

A 30° – 60° – 90° triangle is shown below. Find the length of a and b. Leave answer in simplified radical form. 60° 12 Hint(s) A 309 60° – 90° right triangle is a special type of right triangle where the three angles measure 30 degrees, 60 degrees, and 90 degrees.

Answer 1

Trigonometry

Initial explanation

We have that the sides of a right triangle (depending on the location of the angle we are analyzing), obtain different names:

Finding b

Finding an equation

We want to find b, the information we have is:

angle = 60º

adjacent = 12

hypotenuse = b

The cosine formula uses this information:

`\begin{gathered} \cos (\text{angle)}=\frac{\text{adjacent}}{\text{hypotenuse}} \\ \downarrow \\ \cos (60º)=(12)/(b) \end{gathered}`

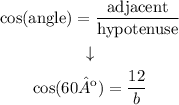
Since cos(60º) = 1/2

`\begin{gathered} \text{cos}(60º)=(12)/(b) \\ \downarrow \\ (1)/(2)=(12)/(b) \end{gathered}`

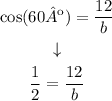
Now, we have an equation that we can use to find b.

Solving the equation

We want to solve the equation for b, that is why we want to "leave it alone" on the left side of the equation.

`\begin{gathered} (1)/(2)=(12)/(b) \\ \downarrow\text{ taking b to the left side} \\ (1)/(2)\cdot b=12 \\ (b)/(2)=12 \\ \downarrow\text{ taking 2 to the right side} \\ b=12\cdot2=24 \end{gathered}`

Then, b = 24 (which is the hypotenuse)

Finding a

Finding an equation

We know that the Sine Equation is given by:

`\sin (\text{angle)}=\frac{\text{opposite}}{\text{hypotenuse}}`

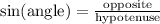
we have the following information:

angle = 60º

opposite = a

hypotenuse = b = 24

Then,

`\begin{gathered} \sin (\text{angle)}=\frac{\text{opposite}}{\text{hypotenuse}} \\ \downarrow \\ \sin (60º)=(a)/(24) \end{gathered}`

since sin(60º) = √3/2

`\begin{gathered} \sin (60º)=(a)/(24) \\ \downarrow \\ \frac{\sqrt[]{3}}{2}=(a)/(24) \end{gathered}`

Now, we have an equation that we can use to find a.

Solving the equation

We want to solve the equation for a,we want to "leave it alone" on one left side

`\begin{gathered} \frac{\sqrt[]{3}}{2}=(a)/(24) \\ \downarrow\text{ taking 24 to the left side} \\ \frac{\sqrt[]{3}}{2}\cdot24=a \\ \frac{24\sqrt[]{3}}{2}=a \\ \downarrow\text{ since 24/2=12} \\ 12\sqrt[]{3}=a \end{gathered}`

Then a = 12√3

Answers: a = 12√3 and b = 24