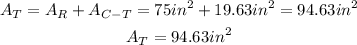Answer:
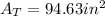
Explanation We need to find the are of the figure provided, the area is composed of three parts, rectangle, and two half circles: therefore the total area would be the sum of the three:
Area Rectangle:
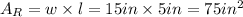
Area of two half circles:
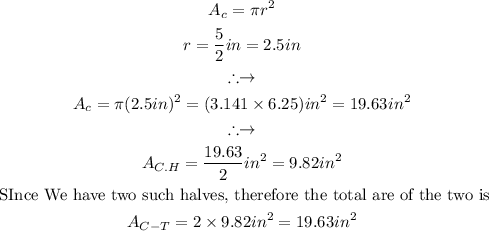
The total area of the figure is: