Question

Suppose we want to choose 5 colors, without replacement, from 8 distinct colors. How many ways can this be done, if the order of the choices is relevant? How many ways can this be done, if the order of the choices is not relevant?

Answer 1

Permutation and combination are two ways of organizing a subgroup of objects extracted from a major group.

We use permutation when the order of the objects of the group matters.

We use combination when the order of the objects does not matters.

Now, let's move on to the problem.

To solve this problem, we can divide it into two steps.

(1) If the order of the choices is relevant.

If the order is relevant, we have to use permutation. The possibilities can be calculated according to the formula:

If r objects are selected from a group of n objects:

`^nP_r=(n!)/((n-r)!)`

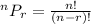
In this exercise,

r = 5

n = 8

Then, let's substitute the values in the formula.

`\begin{gathered} ^nP_r=(8!)/((8-5)!) \\ ^nP_r=(8!)/(3!)=(8\cdot7\cdot6\cdot5\cdot4\cdot3\cdot2)/(3\cdot2) \\ ^nP_r=6720 \end{gathered}`

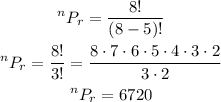
So, if the order is relevant, 6720 choices are possible.

(2) If the order of the choices is not relevant.

If the order is not relevant, we have to use combination. The possibilities can be calculated according to the formula:

If r objects are selected from a group of n objects:

`^nC_r=(n!)/(r!\cdot(n-r)!)`

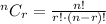
And substituting the values of the exercise:

`\begin{gathered} ^nC_r=(8!)/(5!\cdot(8-5)!)=(8!)/(5!\cdot3!) \\ ^nC_r=(8\cdot7\cdot6\cdot5\cdot4\cdot3\cdot2)/(5\cdot4\cdot3\cdot2\cdot3\cdot2) \\ ^nC_r=56 \end{gathered}`

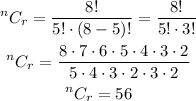
So, if the order is not relevant, 56 choices are possible.

Answer:

Order is relevant: 6720 ways.

Order is not relevant: 56 ways.