Question

The frequency of one string 50 cm long with a diameter of 0.50 mm is 320 Hz. A second string under the same tension and made of the same material is 1.0 m long with a diameter of 0.25 mm. What is the frequency of the second string?

Answer 1

Given data:

* The length of the first string is,

`\begin{gathered} d_1=50\text{ cm} \\ d_1=0.5\text{ m} \end{gathered}`

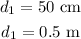
* The diameter of first string is d_1 = 0.5 mm.

* The length of the second string is L_2 = 1 m.

* The diameter of second string is d_2 = 0.25 mm.

* The frequency of first string is f_1 = 320 Hz.

Solution:

The frequency of the first string in terms of length and diameter is,

`f_1\propto(1)/(L_1d_1)\ldots\ldots(1)`

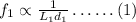
The frequency of the second string in terms of length and diameter is,

`f_2\propto(1)/(L_2d_2)\ldots\ldots....(2)`

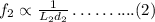
By dividing (2) equation by (1) equation,

`\begin{gathered} (f_2)/(f_1)=((1)/(L_2d_2))/((1)/(L_1d_1)) \\ (f_2)/(f_1)=(L_1d_1)/(L_2d_2) \end{gathered}`

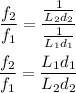
Substituting the known values,

`\begin{gathered} (f_2)/(320)=(0.5*0.5)/(1*0.25) \\ (f_2)/(320)=(0.25)/(0.25) \\ (f_2)/(320)=1 \\ f_2=320\text{ Hz} \end{gathered}`

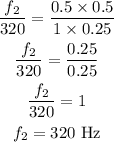
Thus, the frequency of the second string is 320 Hz (same as the frequency of the first string).