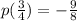Question

3If p(x) = 2x² + 9x -9, find ppl43рП(Type(Type an integer or fraction.)4

Answer 1

In order to determine the value of p(3/4), we just have to replace 3/4 for x, like this:

`\begin{gathered} p((3)/(4))=2((3)/(4))^2+9(3)/(4)-9 \\ \end{gathered}`

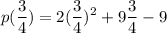
Then, we just have to simplify this expression to determine the vapue of p(3/4), like this:

`\begin{gathered} p((3)/(4))=2(3^2)/(4^2)^{}+9(3)/(4)-9 \\ p((3)/(4))=2(9)/(16)^{}+9(3)/(4)-9 \\ p((3)/(4))=(2*9)/(16)+(9*3)/(4)-9 \\ p((3)/(4))=(18)/(16)+(27)/(4)-9 \\ p((3)/(4))=(9)/(8)+(27)/(4)-9 \end{gathered}`

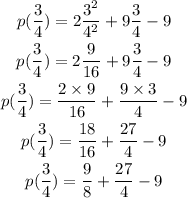
By multiplying the denominator and numerator of the second fraction by 2 we can make the the denominator 8 and add the two fractions:

`\begin{gathered} p((3)/(4))=(9)/(8)+(27*2)/(4*2)-9 \\ p((3)/(4))=(9)/(8)+(54)/(8)-9 \\ p((3)/(4))=(9+54)/(8)-9 \\ p((3)/(4))=(63)/(8)-9 \end{gathered}`

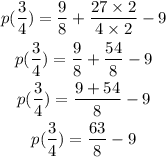
Similarly, by multipling by 8 and dividing by 8 the last term, -9, we get:

`\begin{gathered} p((3)/(4))=(63)/(8)-(9*8)/(8) \\ p((3)/(4))=(63)/(8)-(72)/(8) \\ p((3)/(4))=(63-72)/(8) \\ p((3)/(4))=(63-72)/(8) \\ p((3)/(4))=(-9)/(8) \\ p((3)/(4))=-(9)/(8) \end{gathered}`

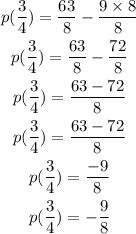
Then, th answer is:

`p((3)/(4))=-(9)/(8)`