We want to continue testing for the zeros of the polynomial given by:

Test for the following integers
![\begin{gathered} x=1\colon1^4-2(1)^3-8(1)^2-32(1)-384 \\ \operatorname{Re}mainder=-425 \\ x=4\colon\text{ 4}^4-2(4)^3-8(4)^2-32(4)-384 \\ \operatorname{Re}mainder=-512 \\ x=16\colon\text{ 16}^4-2(16)^3-8(16)^2-32(16)-384 \\ \operatorname{Re}mainder=54400 \\ x=64\colon\text{ 64}^4-2(64)^3-8(64)^2-32(64)-384 \\ \operatorname{Re}mainder=16217728 \\ x=-4\colon\text{ (-4)}^4-2(-4)^3-8(-4)^2-32(-4)-384 \\ \operatorname{Re}mainder=0 \end{gathered}]()
From the above, -4 is a zero.
Hence,
The factors of the polynomial are:
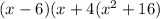
The depressed polynomial obtained is
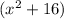
Applying the zero product property, the last zeros will be complex roots
![\begin{gathered} x^2+16=0 \\ \text{subtract 16 from both sides} \\ x^2+16-16=0-16 \\ \text{simplify} \\ x^2=-16 \\ x=\sqrt[]{-16}\text{ or }x=-\sqrt[]{-16}\text{ } \\ x=4i\text{ or }x=4i \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/t9dopdmq3oy7grtecv1yw6st4l461b809o.png)
Synthetic division for zero (x = -4) to prove that it is a zero
Therefore, the function has zeros at +6, -4, 4i and -4i