Question

On a piece of paper, graph y2 X-1. Then determine which answer choice matches the graph you drew. A B C D A. Graph C B. Graph B C. Graph A O D. Graph D PREVIOUS

Answer 1

The equation of a line in Slope-Intercept form is:

`y=mx+b`

Where "m" is the slope of the line and "b" is the y-intercept.

In this case, you have the following inequality:

`y\ge x-1`

Then, the equation of the line is:

`y=x-1`

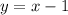
Where the values of "m" and "b" are:

`\begin{gathered} m=1 \\ b=-1 \end{gathered}`

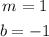
Since the sign of the inequality is:

`\ge`

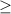
Then the line is solid and the shaded region is above the line.

Knowing the above, you can graph the inequality:

You can see that the line passes through the points (0,-1) and (3,2).

Therefore, the answer is: Option C.