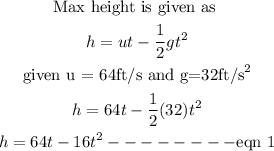
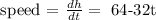
At maximum height , final velocity = 0
Hence
0 = 64-32t
32t=64
t=64/32
t=2
substitute t= 2 into eqn--------------- 1
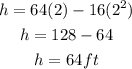
The maximum height covered from below the ground level (in the ditch) is 64ft but Above the ground level, we have 64ft - 12ft which is 52ft above ground level
3. Time taken before the ball hit the ground is obtained by finding the root of
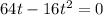
=t (64-16t)=0
64 - 16t=0
16t = 64
t=64/16
t = 4s
Time taken before the ball hit the ground is 4s
4. Vertical velocity before hitting the ground is given as
![\begin{gathered} V\text{ = }\sqrt[]{2gh} \\ V=\text{ }\sqrt[]{2\text{ x 32 x64}} \\ V=32\sqrt[]{2}\text{ ft/s or 45.25ft/3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/dfif15g7dofhncmqqb7nyw3ghcdgt9clc0.png)