We know that
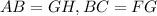
To prove that AC=FH, we need to use the sum of segments property.
According to the given graph, segment AC is formed by
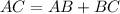
Similarly, FH is defined
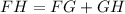
But, we know by given that AB=GH and BC=FG, that means we can replace this on either equation
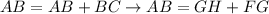
Using the commutative property, we have
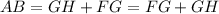
And we know that FH=FG+GH, so
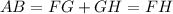
Therefore, AB=FH.