we are given the following measurements for two angles of a triangle
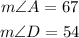
We are asked to find the measure of angle E. Since angle E belongs to the same triangle, if we add the measure of the three angles the result must be 180, that is:
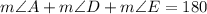
solving for angle E, we get
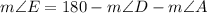
Replacing the known values
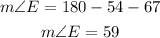
To find then measure of angle BEC, we need to notice that this angle is equal to angle E, therefore:
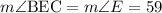
The measure of angle BEC is 59