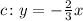Question

Which equation best represents the graph (image is attached) A: y= -3/2xB: y=3/2xC: y= -2/3xD: y= 2/3x

Answer 1

To solve the exercise you can first find the slope of the line using this formula

`\begin{gathered} m=(y_(2)-y_(1))/(x_(2)-x_(1))\Rightarrow\text{ Slope formula} \\ \text{ Where m is the slope and} \\ (x_1,y_1)\text{ and }(x_2,y_2)\text{ are two points through which the line passes} \end{gathered}`

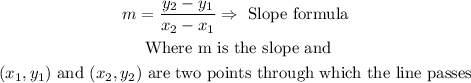
In this case, for example, you can take the points (-3,2) and (0,0). So, you have

`\begin{gathered} (x_1,y_1)=(-3,2) \\ (x_2,y_2)=(0,0) \\ m=(0-2)/(0-(-3)) \\ m=(0-2)/(0+3) \\ m=-(2)/(3) \end{gathered}`

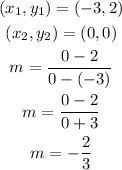
Now, you can use the point-slope formula and solve for y. The point-slope formula is

`y-y_1=m(x-x_1)`

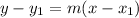
So, you have

`\begin{gathered} y-2=-(2)/(3)(x-(-3)) \\ y-2=-(2)/(3)(x+3) \\ \text{ Apply the distributive property to the right side of the equation} \\ y-2=-(2)/(3)\cdot x-(2)/(3)\cdot3 \\ y-2=-(2)/(3)x-2 \\ \text{ Add 2 from both sides of the equation} \\ y-2+2=-(2)/(3)x-2+2 \\ y=-(2)/(3)x \end{gathered}`

Therefore, the equation that best represents the graph is

`c\colon y=-(2)/(3)x`