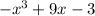The expression is the following:
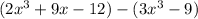
First, we need to evaluate the parenthesis. The first one doesn't have any factors multiplying, dividing or another opration that require it, so we can just remove it:
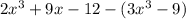
Now, the second parenthesis have a "-" sign in front of it, so we need to distribute this sign to each term inside the parenthesis. We can think of it as multiplying each term by "-1":

No, we pair the like term. Like terms can be classifyied by the x part and its exponent. We have 3 types here, the ones without x, the ones with x to the first (simply x) and the one with x to the third (x³).
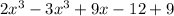
And now we evaluate the like terms to get the simplifyed expression: