Question

Given the function g(x) = 6x ^ 3 + 18x ^ 2 - 144x , find the first derivative, g^ prime (x); g^ prime (x)=

Answer 1

g'(x) = 18x² + 36x - 144

g''(x) = 36x + 36

g''(-4) = -108

At x = -4 the graph of g(x) is concave down

At x = -4 there is a local maximum.

Step-by-step explanation:

The given expression is

`g(x)=6x^3+18x^2-144x`

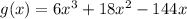
Using the derivative of polynomials, we can find the derivative of g(x) as

`\begin{gathered} g^(\prime)(x)=3(6)x^(3-1)+2(18)x^(2-1)-144 \\ g^(\prime)(x)=18x^2+36x-144 \end{gathered}`

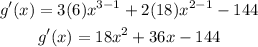
We can verify that g'(-4) = 0 as follows

`\begin{gathered} g^(\prime)(-4)=18(-4)^2+36(-4)-144 \\ g^(\prime)(-4)=18(16)-144-144 \\ g^(\prime)(-4)=288-144-144 \\ g^(\prime)(-4)=0 \end{gathered}`

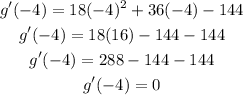
Now, we can calculate the second derivative of g(x), so

`\begin{gathered} g^(\prime)^(\prime)(x)=2(18)x+36 \\ g^(\prime)^(\prime)(x)=36x+36 \end{gathered}`

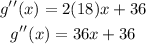
Replacing x = -4, we get:

`\begin{gathered} g^(\prime)^(\prime)(-4)=36(-4)+36 \\ g^(\prime)^(\prime)(-4)=-144+36 \\ g^(\prime)^(\prime)(-4)=-108 \end{gathered}`

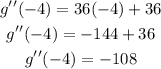
If the second derivative is negative at x = -4, we can say that the graph is concave down and if it is positive, the graph is concave up. In this case, it is -108 which is a negative number, so the graph of f(x) is concave down.

It means that the graph has a local maximum at x = -4.

Therefore, the answers are

g'(x) = 18x² + 36x - 144

g''(x) = 36x + 36

g''(-4) = -108

At x = -4 the graph of g(x) is concave down

At x = -4 there is a local maximum.