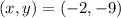Question

Find the solution of this system of equations2x+5y=-49-2x+8y=-68

Answer 1

Given the system of equations :

`\begin{gathered} 2x+5y=-49 \\ -2x+8y=-68 \end{gathered}`

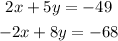
Add the equations to eliminate x :

`\begin{gathered} (2x+5y)+(-2x+8y)=-49+(-68) \\ 2x+5y-2x+8y=-117 \\ (2x-2x)+(5y+8y)=-117 \\ 13y=-117 \end{gathered}`

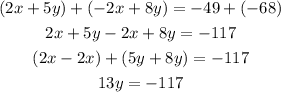
divide both sides by 13 to find the value of y :

`\begin{gathered} (13y)/(13)=(-117)/(13) \\ \\ y=-9 \end{gathered}`

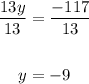
To find x , substitute with the value of y at the first equation :

`\begin{gathered} 2x+5\cdot-9=-49 \\ 2x-45=-49 \\ 2x=-49+45 \\ 2x=-4 \\ \\ x=-(4)/(2) \\ \\ x=-2 \end{gathered}`

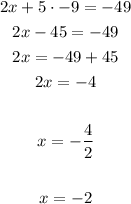
So, the solution of the system is :

`\begin{gathered} x=-2 \\ y=-9 \end{gathered}`

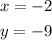
The solution can be written as the order pair (x,y):

`(x,y)=(-2,-9)`