Given: The value of 'a' in y = ax²+bx+c is a=2 and vertex is at (2,0).
Required: To find the x-intercepts.
Explanation: The x-coordinate of the vertex is 2. Also, we know that x-coordinate is given by

Hence, putting the value of x=2 and a=1 we get

Now putting y=0, x=2, a=1, and b=-4 in eq of parabola we get
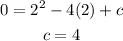
Now the equation of the parabola is,
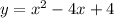
Now to find x-intercepts put y=0 i.e.,

Hence there is only one x-intercept at (2,0). The opening of the parabola can be seen in the graph below-
Final Answer: The parabola has one x-intercept because the parabola opens upward and the vertex is on the x-axis.