NASA launches a rocket at t = 0 seconds. Its height, in meters above sea-level, as a function of time is given by

The sea level is represented by h = 0, therefore, to find the corresponding time when h splashes into the ocean we have to solve for t the following equation:
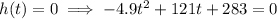
Using the quadratic formula, the solution for our problem is

The rocket splashes after 26.845 seconds.
The maximum of this function happens at the root of the derivative. Differentiating our function, we have
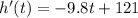
The root is
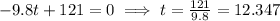
Then, the maximum height is
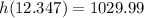
1029.99 meters above sea level.