Question

Margaret drove to a business appointment at 70 mph. Her average speed on the return trip was 60 mph. The return took ⅓ hr longer because of heavy traffic. How far did she travel to the appointment ?

Answer 1

Let d and t be the distance and the time it takes for Margaret to get the place of the appointment.

d is the product of the speed when she was going to the appointment times the time (t):

`d=70t`

d is also the product of the speed when she was going back home times t+1/3:

`d=60(t+(1)/(3))`

Make both d equal and find the value of t:

`\begin{gathered} 70t=60(t+(1)/(3)) \\ 70t=60t+20 \\ 10t=20 \\ t=(20)/(10) \\ t=2 \end{gathered}`

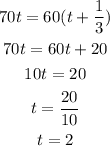
Use this value of t to find d:

`\begin{gathered} d=70(2) \\ d=140 \end{gathered}`

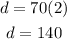
According to this, she traveled 140 miles to the appointment.