Question

A storage bin has the shape of a cylinder with a conical top. What is the volume of the storage bin if its radius is r=5.4 ft, the height of the cylindrical portion is h=7.7 ft, and the overall height is H=16.7 ft?

Answer 1

The Volume of a Compound Solid

The figure consists of a cylinder and a cone, both with the same radius of r=5.4 ft. The height of the cylinder is h=7.7 ft and the total height (of cone and cylinder) is H = 16.7 ft. This means the height of the cone is hc = 16.7 - 7.7 = 9 ft.

The volume of a cylinder of height h and radius r is:

`V_{\text{cyl}}=\pi\cdot r^2\cdot h`

The volume of a cone of height hc and radius r is:

`V_{\text{cone}}=(\pi\cdot r^2\cdot h_c)/(3)`

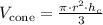
Calculate the volume of the cylinder:

`\begin{gathered} V_{\text{cyl}}=\pi\cdot(5.4ft)^2\cdot7.7ft \\ V_{\text{cyl}}=705.388ft^3 \end{gathered}`

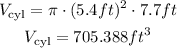
Calculate the volume of the cone:

`V_{\text{cone}}=(\pi\cdot(5.4ft)^2\cdot9)/(3)=274.827ft^3`

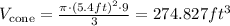
Now we add both volumes:

V = 705.388 + 274.827 = 980.215 cubic feet

Rounding to the nearest tenth:

V = 980.2 cubic feet