For this problem, we are given the expression for a quadratic equation and we need to determine the x-intercepts of its graph.
The x-intercepts coincide with the zeros of the equation, which are obtained when f(x) = 0. So we have:
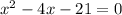
We need to determine the roots of the equation above.
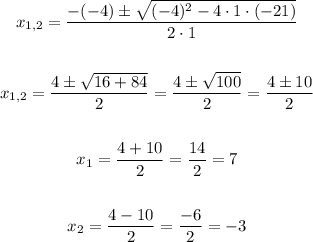
The intercepts are: (-3,0) and (7,0).