Question

3. A boulder rolls with speed of 3.5 m/s off a cliff. It hits the ground 2.25 m from the base ofthe ledge. A) How high is the ledge? B) How long did it take the boulder to fall to the bottomof the cliff?DrawingVerticalHorizontal

Answer 1

Given data

*The given distance from the base of the ledge is R = 2.25 m

*The given speed is v = 3.5 m/s

The diagram is given below

(a)

Let (h) be the height of the edge

The formula for the distance from the base of the ledge is given as

`\begin{gathered} R=v* t \\ R=v*\sqrt[]{(2h)/(g)} \\ h=(R^2* g)/(2v^2) \end{gathered}`

Substitute the known values in the above expression as

`\begin{gathered} h=((2.25)^2*9.8)/(2*(3.5)^2) \\ =2.025\text{ m} \end{gathered}`

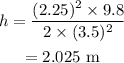
Hence, the height of the ledge is h = 2.025 m

(b)

The formula for the time taken by the boulder to fall to the bottom of the cliff is given as

`t=\sqrt[]{(2h)/(g)}`

Substitute the known values in the above expression as

`\begin{gathered} t=\sqrt[]{(2*2.025)/(9.8)} \\ =0.642\text{ s} \end{gathered}`

Hence, the time taken by the boulder to fall to the bottom of the cliff is t = 0.642 s