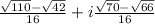Question

Find the quotient Express your answer in standard form,-VIT- iv7-V10 - 116Answer

Answer 1

To make a division of complex numbers, we need to multiply for the conjugate of the denominator:

`(-√(11)-i√(7))/(-√(10)-i√(6))`

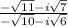
First, we can factor out a (-1) on top and bottom:

`(-√(11)-i√(7))/(-√(10)-i√(6))=((-1)(√(11)+i√(7)))/((-1)(√(10)+i√(6))`

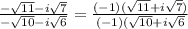
And the two (-1) can cel each other, and now we multiply by the conjugate:

`(√(11)+i√(7))/(√(10)+i√(6))\cdot(√(11)-i√(7))/(√(10)-i√(6))`

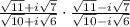
And solve:

`((√(11)+i√(7))(√(10)-i√(6)))/((√(10)+i√(6))(√(10)-i√(6)))=(√(11)√(10)^-i√(6)√(11)+i√(7)√(10)-i^2√(7)√(6))/((√(10))^2+i√(6)√(10)-i√(6)√(10)-i^2(√(6))^2)`

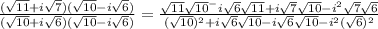
Two terms simplyfy in the denominator, and the square root of the denominator cancel out:

`(√(11\cdot10)^-\imaginaryI√(6\cdot11)+\imaginaryI√(7\cdot10)-(-1)√(7\cdot6))/(10-(-1)\cdot6)`

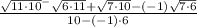
And now we can make the multiplycations:

`(√(110)-i√(66)+i√(70)+√(42))/(16)`

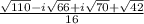
Now we can factor out i, and solve to get the number in the form a + ib

`(√(110)-√(42))/(16)+i(√(70)-√(66))/(16)`