Given the following data:
Principal = $5000
Rate of interest = 8.5%
Time = 9 years
To find the total amount of money that the investor would have after 9 years:
Mathematically, compound interest is given by the formula:
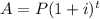
Where,
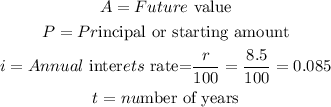
Substituting the given parameters into the formula, we have;
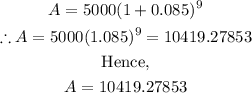
Now, we can find the total amount of money that the investor would have after 9 years:
Total amount of money = Amount + Principal
Total amount of money = 10419.27583 + 5000 = 15419.27853
Therefore,

Hence, the total amount is $ 15,419.