Given:
The mass of the box, m=4 kg
The angle of inclination of the incline, θ=30°
To find:
The normal force, the frictional force, coefficient of friction.
Step-by-step explanation:
Free body diagram of the box;
Where N is the normal force, f is the frictional force, and g is the acceleration due to gravity.
The normal force acting on the box is given by,
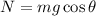
On substituting the known values,
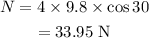
In order to keep the box sliding, the frictional force must at least be equal to the component of the gravitational force that is pulling the box down the incline.
Thus the frictional force needed to keep the box from sliding is,
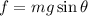
On substituting the known values,
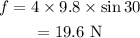
The frictional force is given by,
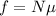
Where μ is the coefficient of frictional force.
On substituting the known values,
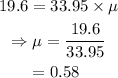
Final answer:
The normal force acting on the box is 33.95 N
The frictional force needed to keep the box from sliding is 19.6 N
The coefficient of frictional force needed is 0.58