Question

How do you determine whether to use plus or minus signs in the binomial factors of a trinomial of the form x^2 + bx + c where b and c may be positive or negative numbers?

Answer 1

The rule of signs in binomial factors given a trinomial in the form :

`x^2\pm bx\pm c`

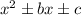
Note that b and c can be positive or negative.

And the factor may be :

`(x\pm m)(x\pm n)`

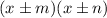
First thing to do is to check the sign of c.

If it is positive, the signs of m and n can be both positive or both negative.

Since positive multiplied by positive is positive and

negative multiplied by negative is also positive.

`\begin{gathered} (+)*(+)=+ \\ (-)*(-)=+ \end{gathered}`

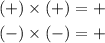
If the sign of c is negative, one of the factors must be negative and the other must be positive, because negative multiplied by positive is negative.

`(-)*(+)=-`

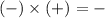
After considering the sign of c, next to check is the sign of b.

Case 1 :

If b and c are both positive, we know that the factors can be both negative or both positive.

And since the sign of b is positive, we must follow the sign of it which is positive.

So both m and n are positive

For example :

`x^2+5x+6`

The factor will be :

`(x+2)(x+3)`

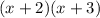
which are both positive.

Case 2 :

If b is negative and c is positive, we will follow the sign of b. m and n will be both negative.

For example :

`x^2-5x+6`

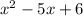
The factors are :

`(x-2)(x-3)`

which are both negative

Case 3 :

Now the third case is tricky.

If c is negative, we know that one of m and n is negative and the other one is positive.

The sign of the larger number between m and n will follow the sign of b.

For example :

`x^2-x-6`

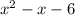
c is negative, so one factor must be negative and the other must be positive. The sign of b is negative, so the larger factor must be negative also.

The factor will be :

`(x-3)(x+2)`

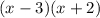
3 is larger than 2, so the negative sign of b will proceed to the factor 3.