Question

Find the axis of symmetry and vertex for the parabola y=−x2+2x+8.

Answer 1

Step 1: Concept

The axis of symmetry always passes through the vertex of the parabola. The x -coordinate of the vertex is the equation of the axis of symmetry of the parabola.

Step 2: Find the axis of symmetry using the formula

`\begin{gathered} The\text{ general expression for a quadratic equation is} \\ y=ax^2\text{ + bx + c } \end{gathered}`

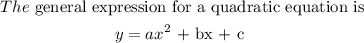
The axis of symmetry is a vertical line.

`\begin{gathered} x\text{ = }(-b)/(2a) \\ y=-x^2\text{ + 2x + 8} \\ a\text{ = -1 , b = 2 and c = 8} \\ x\text{ = }(-2)/(-2) \\ x\text{ = 1} \end{gathered}`

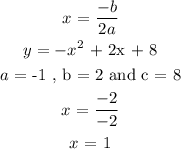
The x -coordinate of the vertex is the equation of the axis of symmetry of the parabola.

Therefore, the axis of symmetry is x= 1

Step 3: Find the vertex

To find the vertex, you substitute x = 1 in the equation of a parabola.

`\begin{gathered} \text{Therefore, we have} \\ y=-x^2\text{ + 2x + 8} \\ y=-1^2\text{ + 2(1) + 8} \\ \text{y = -1 + 2 + 8} \\ y\text{ = 9} \end{gathered}`

The vertex = (1,9)