Step 1: Concept
The axis of symmetry always passes through the vertex of the parabola. The x -coordinate of the vertex is the equation of the axis of symmetry of the parabola.
Step 2: Find the axis of symmetry using the formula
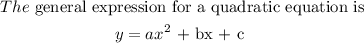
The axis of symmetry is a vertical line.
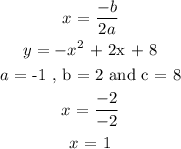
The x -coordinate of the vertex is the equation of the axis of symmetry of the parabola.
Therefore, the axis of symmetry is x= 1
Step 3: Find the vertex
To find the vertex, you substitute x = 1 in the equation of a parabola.
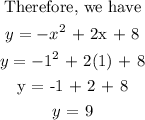
The vertex = (1,9)