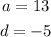Question

I have a sequence question about the difference of arithmetic sequences picture included

Answer 1

The first term and common difference of the 4th term is -2 and the 12th term is -42

The nth term of an arithmetic sequence =

`T_n=a+(n-1)d`

`\begin{gathered} T_4=a+3d=-2............(1) \\ T_(12)=a+11d=-42.........(2) \end{gathered}`

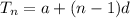
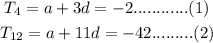
Using elimination method to solve the simultaneous equation

`\begin{gathered} a+3d=-2 \\ \frac{a+11d=-42}{-8d\text{ =40}} \\ d=(40)/(-8) \\ d=-5 \end{gathered}`

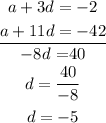
Substitute the value of d in equation 1

`\begin{gathered} a+3d=-2 \\ a+3(-5)=-2 \\ a-15=-2 \\ a=-2+15 \\ a=13 \end{gathered}`

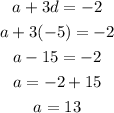
Therefore the correct value are

`\begin{gathered} a=13 \\ d=-5 \end{gathered}`