Given,
The moment of inertia of the wheel, I=0.994 kg·m²
The inner radius of the ring, r=25 cm=0.25 m
The outer radius of the ring, R=35 cm=0.35 m
The force applied by the captain, F=310 N
The force applied by the helmsman, f=286 N
The torque is the measure of the rotation caused by an applied force.
The torque of the wheel is given by,
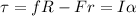
Where α is the angular acceleration of the wheel.
On substituting the known values,

Therefore the angular acceleration of the wheel is 22.7 rad/s²