Question

I need help with 9 please find the area of each shaded sector. Round to the hundredth place.

Answer 1

`A\approx1,330.99ft^2`

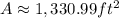
Explanations

The formula for calculating the area of the sector is expressed as:

`A=(\theta)/(360)*\pi r^2`

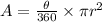
Given the following parameters

`\begin{gathered} \theta=360-(26+90) \\ \theta=360-116 \\ \theta=244^0\text{ (substended angle)} \end{gathered}`

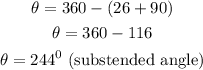
The resulting angle is the sum of the angles of the shaded sectors

Since the radius r = HK = 25ft, hence;

`\begin{gathered} A=(\theta)/(360)*\pi r^2 \\ A=(244)/(360)*\pi(25)^2 \\ A=(244)/(360)*625\pi \\ A=0.6778*1,963.75 \\ A\approx1,330.99ft^2 \end{gathered}`

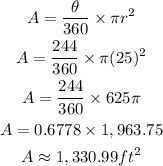
Hence the area of the shaded sectors to the nearest hundredth is 1330.99 square feet