The question is given to be:
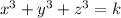
The values for x, y, and z are given below:
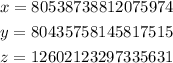
Therefore, we can substitute the values into the equation as shown below:
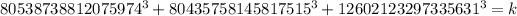
Using a big number calculator, we can calculate the values of the cubic exponents of the numbers to be:
![\begin{gathered} 80538738812075974^3=522,413,599,036,979,150,280,966,144,853,653,247,149,764,362,110,424 \\ 80435758145817515^3=520,412,211,582,497,361,738,652,718,463,552,780,369,306,583,065,875 \\ 12602123297335631^3=2,001,387,454,481,788,542,313,426,390,100,466,780,457,779,044,591 \end{gathered}]()
Therefore, the sum is given to be:
![\begin{gathered} k=522,413,599,036,979,150,280,966,144,853,653,247,149,764,362,110,424+520,412,211,582,497,361,738,652,718,463,552,780,369,306,583,065,875+2,001,387,454,481,788,542,313,426,390,100,466,780,457,779,044,591 \\ k=1,044,827,198,073,958,300,561,932,289,707,306,494,299,528,724,220,890 \end{gathered}]()
The value of k is 1,044,827,198,073,958,300,561,932,289,707,306,494,299,528,724,220,890.