We can see, from the question, that the inverse function of f(x) is given by:
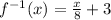
Now, to find f(x), we need to find the inverse function of the given function. To achieve that, we can proceed as follows:
1. Replace x with y as follows:
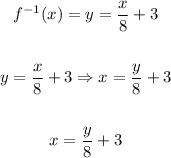
2. Now, we need to solve the expression for y. First, we need to subtract 3 from both sides of the expression:
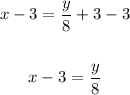
3. We have to multiply both sides of the expression by 8:

Therefore, in summary, we have that the function f(x) is as follows:
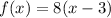
[Option b]