Question

To qualify as a contestant in a race, a runner has to be in the fastest 16% of all applicants. The running times are normally distributed, with a mean of 61 min and a standard deviation of 5 min. To the nearest minute, what is the qualifying time for the race? The qualifying time for the race is _____ min. (Round to the nearest minute as needed.)

Answer 1

We know that the running times are normally distributed and that the time of a runner to qualify has to be in the fastest 16%. From the properties of the normal distribution, we know that:

• Between one and two standards deviation of the mean we have approximately 13.5% of the data.

,

• Between two and three standards deviations of the mean we have approximately 2.35% of the data.

,

• Above three standards deviations of the mean we have 0.15%.

This means that above one standard deviation there are approximately 16% of the data. Then we just need to add one standard deviation to the mean to find the time a runner needs.

`61+5=66`

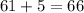
Therefore, the running time to qualify is 66 min