Question

A sample of gas has a pressure of 750 mmHg at 25⁰C what would the new pressure be if the temperature is increased to 125⁰C?

Answer 1

The final pressure of the gas is 1001.6 mmHg

Step-by-step explanation

Given that;

The pressure of the gas is 750 mmHg

The temperature of the gas is 25 degrees celcius

The final temperature of the gas is 125 degrees Celcius

Follow the steps below to find the final pressure of the gas

In the given data, the volume of the gas is fixed, hence, we can apply Gay Lussac's law to find the final pressure of the gas

Step 1; States the Gay Lussac's law

Gay Lussac's a gas law which states that the pressure exerted by a gas (of a given mass and kept at a constant volume) varies directly with the absolute temperature of the gas.

Mathematically, this can be expressed as

`\text{ }\frac{\text{ P1}}{\text{ T1}}\text{ = }\frac{\text{ P2}}{\text{ T2}}`

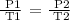
Step 2: Convert the temperature to degrees Kelvin

`\begin{gathered} \text{ T = t}\degree C\text{ + 273.15} \\ \text{ for t1 = 25} \\ \text{ T= 25 + 273.15} \\ \text{ T = 298.15K} \\ \\ \text{ for t2= 125}\degree C \\ \text{ T = 125 + 273.15} \\ \text{ T = 398.15K} \end{gathered}`

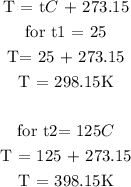
Step 3: Substitute the given data into the formula in step 1

`\begin{gathered} \text{ }\frac{\text{ 750}}{\text{ 298.15}}\text{ = }\frac{\text{ P2}}{\text{ 398.15}} \\ \\ \text{ Cross multiply} \\ \text{ 750}*\text{ 398.15 = 298.15 }*\text{ P2} \\ \text{ 298612.5 = 298.15P2} \\ \text{ Divide both sides by 298.15} \\ \text{ }\frac{\text{ 298612.5}}{\text{ 298.15}}\text{ = }\frac{\text{ 298.15P2}}{\text{ 298.15}} \\ \text{ P2 = 1001.6 mmHg} \end{gathered}`

Therefore, the final pressure of the gas is 1001.6 mmHg