Question

Solve the system of linear equations by elimination, number 2

Answer 1

To solve the system of equations:

`\begin{gathered} 2x+4y=-4 \\ 3x=-5y-3 \end{gathered}`

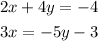
we first write the second equation in standard form, then we have the equivalent system:

`\begin{gathered} 2x+4y=-4 \\ 3x+5y=-3 \end{gathered}`

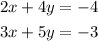
Now we notice that, in the first equation, all the coefficients are multiple of 2 then we can write the system as:

`\begin{gathered} x+2y=-2 \\ 3x+5y=-3 \end{gathered}`

Now, to eliminate one of the variables we need the coefficients of the same variable to be equal in both equations; to achieve this let's multiply the first equation by 3:

`\begin{gathered} 3x+6y=-6 \\ 3x+5y=-3 \end{gathered}`

Now we subtract the second equation from the first and then we have:

`\begin{gathered} 3x+6y-3x-5y=-6-(-3) \\ y=-6+3 \\ y=-3 \end{gathered}`

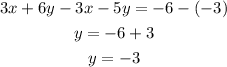
once we know the value of y we plug it in the first equation and solve for x:

`\begin{gathered} x+2(-3)=-2 \\ x-6=-2 \\ x=6-2 \\ x=4 \end{gathered}`

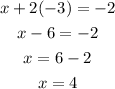
Therefore, the solution for the system of equations is x=4, y=-3