Let's draw the parallelogram in the coordinate plane. This is shown below:
The area of a parallelogram is given by the formula

Where
b is the length of base
h is the height
Let's draw the sides b, h on the diagram:
The length of the base, b, is "5 - 0 = 5 units".
The height, h, is the distance between the points (3,2) and (3, -2). We will use the distance formula to find the length (h).
Distance Formula
![d=\sqrt[]{(y_2-y_1)^2+(x_2-x_1)^2}](https://img.qammunity.org/2023/formulas/mathematics/college/nkjymhkzx142t3t66rnvx6qo7qj0ya3b8k.png)
Where
Given,
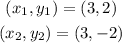
So, the height is:
![\begin{gathered} d=\sqrt[]{(y_2-y_1)^2+(x_2-x_1)^2} \\ h=\sqrt[]{(-2-2)^2+(3-3)^2} \\ h=\sqrt[]{(-4)^2+0} \\ h=\sqrt[]{16} \\ h=4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/c1ueyzaulwcu9gdea7gbc3ln1t0ell6255.png)
We now know, b = 5 units and h = 4 units
Thus, the area of the parallelogram is >>>>
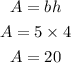
Answer
A. 20 units²