Question

I believe I have the answer correct. I would like to verify the answer thank you! Please confirm answer

Answer 1

We are given the following expression:

`\log \frac{\sqrt[3]{b^2c^4}}{a^8}`

To determine the numerical value of the expression we will use different "log" properties to expand it.

First, we will use the following property:

`\log (x)/(y)=\log x-\log y`

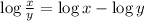
Applying the property we get:

`\log \frac{\sqrt[3]{b^2c^4}}{a^8}=\log \sqrt[3]{b^2c^4}-\log a^8`

Now, we will use the following property of roots:

`\sqrt[n]{x}=x^{(1)/(n)}`

Applying the property we get:

`\log \sqrt[3]{b^2c^4}-\log a^8=\log (b^2c^4)^{(1)/(3)}-\log a^8`

Now, we use the following property:

`\log x^n=n\log x`

Applying the property:

`\log (b^2c^4)^{(1)/(3)}-\log a^8=(1)/(3)\log b^2c^4-8\log a`

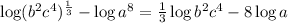
Now, we apply the following property on the "log" on the left side:

`(1)/(3)\log b^2c^4-8\log a=(1)/(3)\log (b^2)+(1)/(3)\log c^4-8\log a`

Now, we apply the property of exponents:

`(1)/(3)\log (b^2)+(1)/(3)\log c^4-8\log a=(2)/(3)\log (b^{})+(4)/(3)\log c^{}-8\log a`

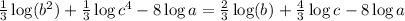
Now, we substitute the given values for each of the "log":

`(2)/(3)\log (b^{})+(4)/(3)\log c^{}-8\log a=(2)/(3)(-9)+(4)/(3)(-9)-8(-10)`

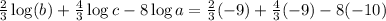
Solving the operations:

`(2)/(3)(-9)+(4)/(3)(-9)-8(-10)=62`

Therefore, the numerical value of the expression is 62.