Answer:
Graph C
Explanation:
Given the inequality:
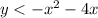
• The ,coefficient of x² is negative,, so the parabola ,opens downwards.
,
• This means either Option C or D is correct.
However, considering the critical points of the boundary line:
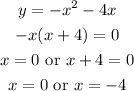
The line must intersect the x-axis at x=0 and x=-4.
This corresponds to the x-intercepts in Graph C.
Graph C is the correct graph.