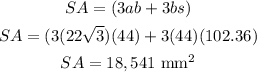Answer:
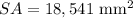
Explanation:
The surface area of a regular hexagonal pyramid is represented by the following equation:
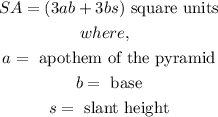
Therefore, if the height of the award is 95 millimeters and the base edge is 44 millimeters.
Since it is a regular hexagon, the apothem is formed by an equilateral triangle, therefore using the Pythagorean theorem:
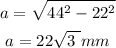
Now, for the slant height, use the Pythagorean theorem too using the apothem and the given height:
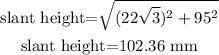
Now, solve the equation of the surface area: