Hello there. To solve this question, we'll have to remember some properties about cost and profit functions.
Given the cost C of producing q goods as the function:
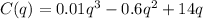
a) What is the fixed cost?
For this, we'll have to evaluate the function C at the number of goods q for which it doesn't change, in other words:
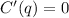
Differentiating the function with respect to q, we get:
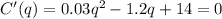
Solving this quadratic equation, we get:
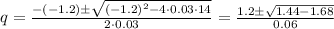
Since this will give us
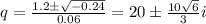
That is a complex number, so it doesn't have real solutions.
Therefore there isn't a fixed cost for this function.
b) What is the maximum profit if each item is sold for 10 dollars?
For this, we'll need to define the profit function P(q) as follows:
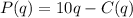
That is, 10 dollars multiplied by the number of goods sold, minus the cost production of the goods.
This gives us:
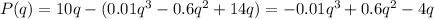
Now we have to differentiate that function and determine its critical points.
That is, the points q where P'(q) = 0.
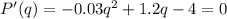
Solving this quadratic equation leads to
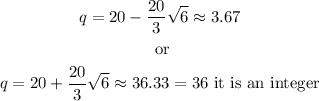
Hence we differentiate it again and determine for which of these value we get P''(q) < 0
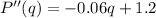
Evaluating this at the points we found, we get:
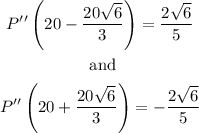
This gives us that q = 36.33 might be the number of goods that gives us the maximum profit, that is
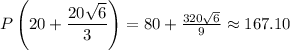
Now, suppose we fix at 36 goods production, and that they sell when the price is 10 dollars each. Also suppose that for each 1 dollar increase in price, 2 fewer goods are sold (so if the price is 11 dollars, 34 of the 36 goods are sold).
To maximize profit in this case, we have to determine the variable r such that when the price is
10 + r, then the function P(q-2r) gives maximum profit.
Notice that when we add r dollars to the price, twice its amount is not being sold, therefore:
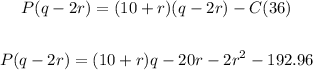
Notice the cost doesn't change because in this case we still produce q units (in fact, 36 because we fixed it).
Now, we determine the max of this function with respect to r when q = 36
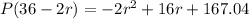
This is a quadratic function, hence its max is at the vertex, thus
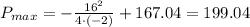
And this happens when
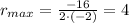
So the price should increase by 4 dollars.